Assignment Code: MCS-212/Assign/2024

Course Code: MCS-212

Assignment Name: Discrete Mathematics

Year: 2024

Verification Status: Verified by Professor

This expression is in the form of the formula we wanted to prove, but for  instead of . Hence, by mathematical induction, the formula holds for all positive integers .

Q2) How many different permutations are possible of the letters, taken all at a tune, of the word: ASSESSES?

Ans) The word "ASSESSES" contains 8 letters, with the letter "S" appearing 4 times and the letter "E" appearing twice.  

Permutation formula

The number of permutations of n objects, where m1 objects are of one kind, m2 are of the second kind, …, mk is of kth type and the rest, if any, are of a different kind,

Q3) A die is rolled once. What are the probabilities of the following events:

a. Getting an odd number

b. Getting at least a value 2

c. Getting at most a value 2

d. Getting at least 7

Ans) Probability of an event is given by

Getting an odd number:

When a die is thrown, the total possible outcomes are 1, 2, 3, 4, 5 and 6.number of possible outcomes = 6

There are three odd numbers on a six-sided die: 1, 3, and 5.number of favorable outcomes = 3

Probability of getting an odd number = 3/ 6 = 1/2

Getting at least a value 2:

The values 2, 3, 4, 5, and 6 are all at least 2.

number of favorable outcomes = 5

Probability of Getting at least a value 2 = 5 /6

Getting at most a value 2:

The values 1 and 2 are at most 2.

number of favorable outcomes = 2

Probability of getting at most a value 2 = 2 / 6 = 1/3

Getting at least 7:

It's impossible to get a value of at least 7 on a standard six-sided die since the maximum value is 6.

number of favorable outcomes = 0

Probability of ggetting at least 7 = 0

Q4) Draw a hypercube graph Q3 (also called the cubical hypercube). Check whether the hypercube Q3 is Hamiltonian.

Ans) Hypercube graph Q3

To check whether the hypercube Q3 is Hamiltonian, we need to determine if there exists a Hamiltonian cycle in the graph, i.e., a cycle that visits each vertex exactly once.

The gray code ordering of vertices is

000 (0)

001 (1)

011 (3)

010 (2)

110 (6)

111 (7)

101 (5)

100 (4)

All adjacent numbers differ by exactly one bit. The last and first numbers also differ by one bit. Thus, the above sequence forms a Hamiltonian circuit.

Q5) What is isomorphism? Find, if the following graphs G1 and G2 are isomorphic or not. Explain how you arrived at your answer.

Ans) In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H

f:V(G)→V(H)

such that any two vertices u and v of G are adjacent in G if and only if f(u)

and f(v) are adjacent in H.

This kind of bijection is commonly described as "edge-preserving bijection", in accordance with the general notion of isomorphism being a structure-preserving bijection.

Any two graphs will be known as isomorphic if they satisfy the following four conditions:

There will be an equal number of vertices in the given graphs.

There will be an equal number of edges in the given graphs.

There will be an equal amount of degree sequence in the given graphs.

If the first graph is forming a cycle of length k with the help of vertices {v1, v2, v3, …. vk}, then another graph must also form the same cycle of the same length k with the help of vertices {v1, v2, v3, …. vk}.

Condition 1:

In G1, total number of vertices = 4

In G2, total number of vertices = 4

Condition 2:

In G1, total number of edges = 6

In G2, total number of edges = 6.

Condition 3:

In G1, the degree of sequence = {3, 3, 3, 3}

In G2, the degree of sequence = {3, 3, 3, 3}

Condition 4:

G1 forms a cycle of length 3 with the help of vertices {3, 3, 3}.

G2 also forms a cycle of length 3 with the help of vertices {3, 3, 3}.

Q6) What is a finite automata? Why is it needed? How is a finite automata represented? Also explain the term regular expression with the help of an example.

Ans) Finite automata are simple abstract machines used to recognize patterns. It is a mathematical model of a system with discrete inputs, output, states, and a set of transitions from state to state that occurs on input alphabets symbols.

Need

Finite automata are needed for several reasons:

Lexical Analysis:

Finite automata are extensively used in compiler design for lexical analysis, which involves tokenizing and scanning the source code of a programming language. Lexical analyzers employ finite automata to recognize and classify different lexical units such as keywords, identifiers, operators, and literals.

Pattern Recognition:

Finite automata are employed in pattern-matching and recognition tasks. They can be used to search for specific patterns or sequences of characters within a given input. Applications include text processing, string matching, and searching algorithms.

Network Protocol Analysis:

Finite automata are used in network protocol analysis and packet filtering. They can be employed to define rules and match patterns in network traffic, enabling functionalities like intrusion detection, firewalls, and network monitoring.

Methods of Representation

The finite automata can be represented in three ways, as given below

1.      Graphical (Transition diagram)

2.     Tabular (Transition table)

3.     Mathematical (Transition function)

Regular expression

A regular expression is an algebraic formula whose value is a pattern consisting of a set of strings, called the language of the expression. Just as finite automata are used to recognize patterns of strings, regular expressions are used to generate patterns of strings.

The below regular expression can be used for checking if a given set of characters is an email address or not. 

^[a-zA-Z0-9._-]+@[a-zA-Z0-9.-]+\.[a-zA-Z]{2,4}$

Key components of the regex pattern:^: Start of the string.

[a-zA-Z0-9._-]+: Match one or more alphanumeric characters, dots, underscores, or hyphens for the username part.

@: Match the "@" symbol.

[a-zA-Z0-9.-]+: Match one or more alphanumeric characters, dots, or hyphens for the domain name.

\.: Match a period (dot), which separates the domain name and top-level domain (TLD).

[a-zA-Z]{2,4}: Match the TLD, consisting of 2 to 4 alphabetical characters.

$: End of the string.

Q7) Differentiate between

a. Deterministic and Non-deterministic finite automata

Ans)

Q7. b. Deterministic and Non-deterministic Turing Machine

Ans) Deterministic Turing Machine (DTM) and Non-deterministic Turing Machine (NTM) are two variations of the Turing Machine, a theoretical model of computation developed by Alan Turing in the 1930s. They have some fundamental differences:

Q7. c. Moore and Mealy Machine

Ans)

Q8) Describe the divide-and-conquer approach to solve recurrences? Explain how this approach can be used to apply binary search in a sorted list.

Ans) The divide-and-conquer approach is a problem-solving strategy that involves breaking a problem into smaller subproblems, solving each subproblem recursively, and then combining the solutions to the subproblems to solve the original problem.

Here's a general outline of how the divide-and-conquer approach can be applied to solve recurrences:

Divide

Break the problem into smaller subproblems. This step typically involves dividing the problem instance into two or more smaller instances.

Conquer

Solve the subproblems recursively. Apply the same algorithm to each subproblem until reaching base cases, which are small enough to be solved directly.

Combine

Combine the solutions of the subproblems to solve the original problem. This step involves aggregating the solutions of the subproblems into a solution for the original problem.

The divide-and-conquer approach can be used to implement binary search in a sorted list.

Binary search is an efficient algorithm for finding a target value within a sorted array or list. It works by repeatedly dividing the search interval in half and narrowing down the possible locations of the target value.

Binary search can be implemented using the divide-and-conquer approach.

Divide: Given a sorted list, divide it into two halves.

Conquer: Compare the target value with the middle element of the list. If the target value is equal to the middle element, the search is successful. If the target value is less than the middle element, recursively search the left half of the list. If the target value is greater than the middle element, recursively search the right half of the list.

Combine: If the target value is found, return its index. If the search interval is empty (indicating that the target value is not present in the list), return a "not found" indicator.

By repeatedly dividing the search interval in half and discarding the half that cannot contain the target value, binary search efficiently locates the target value in logarithmic time complexity (O(log n)), where n is the size of the list. This makes it significantly faster than linear search for large lists.

Q9) What is proposition? Explain with the help of an example. Explain Disjunction and Conjunction with the help of truth table for each.

Ans) In logic, a proposition is a statement that can either be true or false, but not both. It is a declarative sentence that asserts something about the world.

Example,

"The sky is blue" is a proposition because it can be either true or false depending on the current state of the sky.

Disjunction (OR)

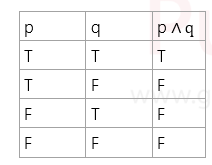
Disjunction is a logical operation that evaluates to true if at least one of the propositions it connects is true. The symbol for disjunction is "∨" (pronounced "or").

Truth table for disjunction

Example: Let's say p represents the proposition "It is raining" and q represents the proposition "It is sunny". The disjunction "p ∨ q" would be true if it is either raining, sunny, or both.

Conjunction (AND)

Conjunction is a logical operation that evaluates to true only if both of the propositions it connects are true. The symbol for conjunction is "∧" (pronounced "and").

Example: Using the same propositions as before, "p ∧ q" would be true only if it is both raining and sunny simultaneously.

Q10) Prove the following theorem by direct proof method: "The square of an even integer is an even integer.

Ans) Direct Proof:

Suppose n is an even integer.

By definition, an even integer can be expressed as  where  is an integer  squaring both sides since  is of the form , we can see that  is divisible by

Therefore,  is an even integer.

Q11) Given the Boolean expression (a' v (b A c')) v (b v d'), draw the corresponding circuit, where a, b, c and d are the inputs to the circuitry.

Ans)

Q12) Define the terms Domain, Co-domain and Range in the context of a function. Also find the domain, co-domain and range for a function A to B, where A={1,2,3,4} and B={ 1, 4, 9, 16, 25}

Ans) Domain:

The domain of a function is the set of all possible input values (or independent variables) for which the function is defined. It represents the values that can be plugged into the function.

Co-domain:

The co-domain of a function is the set of all possible output values (or dependent variables) that the function can produce.

Range:

The range of a function is the set of all actual output values produced by the function when the elements of the domain are inputted.  

Domain, co-domain and range for a function A to B, where A={1,2,3,4} and B={ 1, 4, 9, 16, 25}

Q13) A committee consisting of 2 male and 2 female workers is to be constituted from 8 male and 9 female workers. In how many distinct ways can this be done?

Ans) Combinations formula

Q14) In a tennis tournament, each entrant plays a match in the first round. Next, all winners from the first round play a second-round match. Winners continue to move on to the next round, until finally only one player is left as the tournament winner. Assuming that tournaments always involve n=2^k players, for some k, find the recurrence relation for the number rounds in a tournaments of n players.

Ans) The tournament can be subdivided into 2 sub tournaments of n/2 players each.

After a_(n\/2) rounds, one player will be left in both the sub tournaments. The winner of the match betwen two is the winner of the tournament.

So, the recurrence relation is

no. of rounds played in a tournament = 2 x number of rounds played in sub tournaments of n/2 players each + 1

a_n=2a_(n\/2)+1

Q15) Show, using the pigeonhole principle, that in any group of 30 people, 5 people can always be found who were born on the same day of the week.

Ans) The “Generalized” Pigeonhole Principle is as follows:

If kn + 1 objects are placed in n boxes, then some box contains at least k+1 objects.

We have,

n= 7 boxes (weekdays)

kn+1=30 objects (people)

kn+1=4.28(7)+1

k = 4

k+1 = 4+1=5

Therefore, 5 people can always be found who were born on the same day of the week.

Q16) Define the following in the context of graph, with the help of an example

a. Complete graph

Ans) Complete graph

A complete graph is a simple graph in which every pair of distinct vertices is connected by a unique edge.

b. Degree of a vertex

Ans) The degree of a vertex in a graph is the number of edges incident to that vertex.

Example: Consider the graph G with vertices A, B, C, D, E and edges AB, AC, AD, AE. The degree of vertex A is 4 because it is incident to 4 edges.

c. Cycle

Ans) A cycle in a graph is a closed path where the first and last vertices are the same, and no vertex (except the first and last) is repeated.

Example: In the graph G with vertices A, B, C, D, E and edges AB, BC, CD, DE, EA, the cycle ABCDEA forms a closed loop.

d. Path

Ans) A path in a graph is a sequence of vertices in which each vertex is adjacent to the next one in the sequence by an edge.

Example: In the graph G with vertices A, B, C, D, E and edges AB, BC, CD, DE, the path  forms a sequence of vertices connected by edges.

e. Circuit

Ans) A circuit in a graph is a closed path where the first and last vertices are the same, and no vertex (except the first and last) is repeated. Additionally, all edges in the circuit must be distinct.

Example: In the graph G with vertices A, B, C, D, E and edges AB, BC, CD, DE, EA, the circuit ABCDEA forms a closed loop where each edge is distinct.

Q17) What is a bipartite graph? Explain with the help of an example. Give one or two applications of bipartite graphs.

Ans) A Bipartite Graph is a type of graph in which we can partition the whole graph into two Bipartite Sets such that edges connect vertices present in one set to vertices in another set. A bipartite Graph does not have any edge which connects the vertex of one set to the vertex present in the same set.

Example 

The above graph contains a cycle of length 6 and the vertices or nodes can be divided into two sets i.e., {A, C, E} and {B, D, F}, such that every edge connects a vertex in one set to a vertex in the other set. This graph confirms to all the conditions of a bipartite graph. Therefore, this graph is also a bipartite graph.

Applications of Bipartite Graph

Bipartite Graphs are used in several fields. Some of the applications of Bipartite Graphs are given below.

Bipartite Graphs are used to solve the Matching Problems. For example, it can be used for assigning employees a number of tasks or assigning students to different courses.

Bipartite graphs can be used to make recommendation systems, where one set of vertices represents users and the other set represents items. If a user has rated an item, an edge is drawn between the corresponding vertices. The goal is to recommend items to users based on their preferences.

Bipartite graphs, in which one set of vertices represents people and the other set represents groups, can be used to model social networks. If the user is a member of the group, an edge is drawn between them.

Q18) How Hamiltonian graphs differ from the Eulerian graphs? Give Dirac's and Ore's criterion for the Hamiltonian graphs.

Ans) Hamiltonian graphs and Eulerian graphs are both types of graphs studied in graph theory, but they differ in terms of the properties they possess.

Hamiltonian Graphs

a) A Hamiltonian graph is a graph that contains a Hamiltonian cycle, which is a cycle that visits every vertex exactly once and returns to the starting vertex.

b) In other words, a Hamiltonian cycle is a closed loop that travels through every vertex in the graph exactly once.

c) Hamiltonian graphs are named after Sir William Rowan Hamilton, an Irish mathematician.

d) Determining whether a graph is Hamiltonian is an NP-complete problem, meaning there is no known efficient algorithm to solve it for all cases.

Eulerian Graphs

a) An Eulerian graph is a graph that contains an Eulerian circuit, which is a closed walk that covers every edge exactly once and returns to the starting point.

b) In other words, an Eulerian circuit is a closed loop that travels along every edge in the graph exactly once.

c) Eulerian graphs are named after Leonhard Euler, a Swiss mathematician.

d) Unlike Hamiltonian graphs, it's often easier to determine whether a graph is Eulerian. A necessary and sufficient condition for a graph to be Eulerian is that every vertex has an even degree.

Dirac's and Ore's criterion for the Hamiltonian graphs

Q19) Differentiate between Eulerian graph and Eulerian circuit. Find the Eulerian circuit in the graph given below (if it exists).

Ans) Eulerian graph

An Eulerian graph is a graph that contains a closed walk (a path that starts and ends at the same vertex) that traverses each edge of the graph exactly once. This closed walk is called an Eulerian circuit.

Eulerian circuit

An Eulerian circuit is a closed walk in a graph that traverses each edge exactly once and returns to the starting vertex. It is also referred to as an Eulerian cycle.

An undirected graph has Eulerian circuit if following two conditions are true.

All vertices with non-zero degree are connected.

All vertices have even degree.

The given undirected graph has Eulerian circuit as

All vertices with non-zero degree are connected.

All vertices have even degree (4, 2, 4, 2, 4, 2)

Here, Eulerian circuit is {a, c, e, a, b, c, d, e, f, a}

Q20) Write Short notes on following

a. Travelling Salesman Problem

Ans) The travelling salesman problem is a graph computational problem where the salesman needs to visit all cities (represented using nodes in a graph) in a list just once and the distances (represented using edges in the graph) between all these cities are known.

The solution that is needed to be found for this problem is the shortest possible route in which the salesman visits all the cities and returns to the origin city.

Considering that the salesman starts from the vertex ‘a’, they need to travel through all the remaining vertices b, c, d, e, f and get back to ‘a’ while making sure that the cost taken is minimum.

There are various approaches to find the solution to the travelling salesman problem: naive approach, greedy approach, dynamic programming approach, etc.

The Traveling Salesman Problem is a classic optimization problem with significant theoretical and practical importance.

b. Vertex Colouring

Ans) Vertex colouring is a concept in graph theory that refers to assigning colours to the vertices of a graph in such a way that no two adjacent vertices have the same colour.

Formally, the vertex colouring of a graph is an assignment of colours. We usually represent the colours by numbers. Additionally, we assign the colors to the vertices such that two adjacent vertices are always filled with different colours.

Furthermore, the minimum number of colours we require to colour the vertices of a graph is known as the chromatic number. Generally, this number is always greater than one. However, the chromatic number is equal to one if and only if the graph contains a single vertex.

The concept of vertex colouring is used in many areas of computer science and mathematics. Additionally, we can model complex real-life problems to the vertex colouring problem.

Finding the chromatic number of a graph is difficult and belongs to the NP-complete class. Hence, it’s unlikely that there’s an efficient algorithm to solve it for all graphs. However, for certain special classes of graphs, efficient algorithms exist.

c. Edge Colouring

Ans) Edge colouring is a fundamental concept in graph theory that involves assigning colours to the edges of a graph in such a way that no two adjacent edges share the same colour.

Several algorithms have been developed to find edge colourings efficiently. Greedy algorithms, backtracking techniques, and integer linear programming are commonly used approaches to solve edge colouring problems.

Edge colouring has numerous applications in real-world scenarios such as scheduling tasks to minimize conflicts, allocating resources efficiently, and organizing timetables. It's used in various domains including computer science, telecommunication, transportation, and manufacturing.

d. Planar graphs

Ans) A graph is said to be planar if it can be drawn in a plane so that no edge cross. 

A planar graph divides the plane into one or more regions. One of these regions will be infinite.

Finite Region: If the area of the region is finite, then that region is called a finite region.

Infinite Region: If the area of the region is infinite, that region is called a infinite region. A planar graph has only one infinite region.

Properties of Planar Graphs:

If a connected planar graph G has e edges and r regions, then r ≤2/3 e

If a connected planar graph G has e edges, v vertices, and r regions, then v-e+r=2.

If a connected planar graph G has e edges and v vertices, then 3v-e≥6.

A complete graph Kn is a planar if and only if n<5.

A complete bipartite graph Kmn is planar if and only if m<3 or n>3.

Planar graphs are used in diverse fields such as computer science, mathematics, and network design.

e. Pascal's Formula