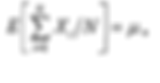Assignment Code: MECE-003/AST/2021-22

Course Code: MECE-003

Assignment Name: Actuarial Economics: Theory and Practice

Year: 2021-2022 (July 2021 and January 2022)

Verification Status: Verified by Professor

Note: Answer all the questions. While questions in Section A carry 20 marks each (to be answered in about 500 words each) those in Section B carry 12 marks each (to be answered in about 300 words each). In the case of numerical questions word limits do not apply.

Section A

1) State and explain the significance of ‘convergence and limit laws’.

Ans) We have already seen that the mean and variance of two independent random variables X and Y:

and

More generally, if X1,..., XN, are N independent random variables, we have mean

and variance

Note that we only use the independence for the variance. Without independence the mean is unchanged, but the variance becomes

Independence ensures that all the covariance terms in the double sum are equal to zero. Supposing all random variables to be independent and have the same mean p, variance 02. Then the sum has mean

and variance

The mean and variance of the average are

and

Examine the behaviour of the average of the first N random variables

Examine the behaviour of the average of the first N random variables

as N gets large. In that Ease the variance of the sample average gets smaller and smaller. Using Chebyshev's inequality, this implies that the

Note that in the first example the convergence is clearly in quadratic Linear and probability. The independence implies it is also convergence almost surely. The following relations hold between the different convergence concepts:

1. Convergence in quadratic mean implies convergence in probability.

2. Convergence almost surely implies convergence in probability.

3. Convergence in quadratic mean does not imply, and is not implied by, convergence almost surely.

Difference between convergence in quadratic mean and convergence almost surely.

2) Discuss the various aspects of insurance sector that are regulated.

Ans) The insurance industry in India dates back to the early 1800s and has grown over the years with better transparency and focus on protecting the interest of the policyholder. The IRDA plays an integral role in emphasizing the importance of policyholders and their interest while framing rules and regulations. Here are the important roles of the IRDA:

1. To protect the policyholder’s interests.

2. To help speed up the growth of the insurance industry in an orderly fashion, for the benefit of the common man.

3. To provide long-term funds to speed up the nation’s economy.

4. To promote, set, enforce and monitor high standards of integrity, fair dealing, financial soundness and competence of the insurance providers.

5. To ensure genuine claims are settled faster and efficiently.

6. To prevent malpractices and fraud, the IRDA has set up a grievance redress forum to ensure the policyholder is protected.

7. To promote transparency, fairness and systematic conduct of insurance in the financial markets.

8. To build a dependable management system to make sure high standards of financial stability are followed by insurers.

9. To take adequate action where such high standards are not maintained.

10. To ensure the optimum amount of self-regulation of the industry.

Functions of IRDA:

Below are the important functions of the IRDAI in the insurance industry in India:

1. Grant, renew, modify, suspend, cancel or withdraw registration certificates of the insurance company.

2. Protecting the interests of the policyholder in matters concerning the grant of policies, settlement of claims, nomination by policyholders, insurable interest, surrender value of the policy and other terms and conditions of the policy.

3. Specify code of conduct, qualifications and training for intermediary or insurance agents.

4. Specify code of conduct for loss assessors and surveyors.

5. Levying fees and charges for carrying out the provisions of the Act.

6. Undertaking inspection, calling for information, and investigations including an audit of insurance companies, intermediaries, and other organizations associated with the insurance business.

7. Regulate and control insurance rates, terms and conditions, advantages that may be offered by the insurance providers.

8. Apart from the above-mentioned core functions of the IRDA, there are several functions that the regulator performs keeping the policyholder’s interest as its priority.

9. Insurance is mainly divided into Life and Non-Life/General Insurance. These are further classified into other types of insurance. Below are the types of insurance regulated by the IRDAI:

   
   

Life Insurance

Term Plans

Endowment Policies

Unit-linked Insurance Policies

Retirement Policies

Money-back Policies

General Insurance

Health Insurance Policies

Vehicle/Motor Insurance Policies

Car insurance

Bike Insurance

Property Insurance Policies

Travel Insurance Plans

Gadget Insurance Plans

Section B

3) Explain the elements of ‘interest calculation’ with examples.

Ans) Interest rate is the time value of money. As an insurance contract's due insured pays the insurer a fixed premium periodically, annually to semi-annually, the present and future value of such payments needs to be balanced. Thus, $1 in hand today is to be viewed as more valuable than $1 you would receive one year later. Insurance companies take this into account.

We are familiar with the computation of compound interest. It runs as follows: an amount A is invested at interest rate i per year. At the end of the period, the amount will be A + iA = d(1+ i) subject to the condition that the interest is compounded annually. For the computation of second year amount, the interest earned during the first year enters along with the principal.

In such a process, after n years, the amount will be A(I + i)n . Note that the accumulation factor is    (1 + i)n . We derive the nominal annual rate of interest, if the interest is compounded daily so that after n years the amount becomes

Example 1.

Suppose that there prevails an interest rate of 5% compounded quarterly. Find the effective rate of interest.

Example 2.

You are interested to invest $1 for which two banks A and B are willing offer two types of compounded process. While A pays 5% interest compounded monthly, B follows a process of compounding daily and offers an interest that makes you indifferent between selecting the banks. What is the interest rate in B that makes you equally attractive for your investment plan?

Suppose that your investment is for t years. Then the amount to be given by A and B will be

4) What is a ‘life annuity contract’? How is its ‘actuarial present value’ determined?

Ans) A Life Annuity contract is an agreement to pay a scheduled payment to the policyholder. It needs to be paid at every interval

of a year while the annuitant is alive up to a maximum number of nm payments.

See that these are contingent annuities in which payments are made for a random, time interval. To appreciate the idea, suppose that in a life insurance policy, (x) pays a premium at the beginning of each year until the time of death. Thus, the premium payments represent a life annuity due for (x). Take a case in which the payment amount is 1. As the premiums are paid annually, the term of this life annuity depends on the curtate life of (x) and there will be K (x) + I payments. We can write the actuarial present value of the payments

Note that the above formulation gives the relationship between this life annuity due and the net single premium for a whole life policy. Let us consider the actuarial present value of a life annuity immediate. Here the first payment is made at the

and the last payment at time n in the case of a finite term n over which the annuitant survives. Thus,

When a life annuity due in which payments are made m times per year and each payment is l/m the actuarial present value denoted by ax(m). In such a case, there are, mT+1 payments. Therefore,

An annuity is called a temporary life annuity, when pension benefits are in the form of a life annuity immediate. In this arrangement the insured exercises the option of receiving a higher benefit only for a fixed number of years or unit death occurs depending on whichever comes first.

Consider a situation of annuities payable continuously. Suppose that the rate of benefit payment is constant and is 1 per unit time. Then in a time interval (t,d +dt), the amount paid is dt and its present value is e-st dt . Thus, the present value of the continuously paid annuity over a period of n years would be

A  life annuity payable continuously will have actuarial present value

Consider  the case of an insurer selling a fully discrete whole life policy. . It will be paid for by equal annual premium payments during the life of the insured. Note that filly discrete refers to the fact that the benefit is to be paid at the end of the year of death and the premiums are to be paid on a discrete basis as well. We turn to the idea behind the pricing of life insurance, that is, premium calculation. A first approximation yields the net premium, which is found by the equivalence principle: It says, the premium should be set such that the actuarial present value of the benefits paid is equal to the actuarial present value of the premiums received. On the basis of this principle, therefore, the net premium P should satisfy

or, Ax-pax=0.

To find the net premium, p30, for (30) if i = 0.05, we take the help of a life table. It can be shown in that p30 = A30 l a30 = 0.10248/15.8561. You many extend net premiums for fully discrete insurances.

6) State the key components of ‘extreme value theory (EVT)’ with a particular reference to the ‘generalised extreme value (GEV) distribution’.

Ans)

GEV Distribution

The Frechet distribution corresponds to fat-tailed distributions and has been found to be the most appropriate for fat-tailed financial data. Since the asymptotic distribution of the maximum always belongs to one of these three distributions, irrespective of the original distribution we should note the importance of this result. The asymptotic distribution of the maximum can be estimated without making any assumptions about the nature of the original distribution of the observations.

Procedure for Tail Estimation

You May note that the purpose of tail estimation procedures is to estimate the values of X outside the range of existing data. To do this, we have to employ both extreme events and exceedances of a .specified level. The standard approach assumes that the tail of the population follows the selected family of distribution as seen above and we will discuss more in the following. 1

Maximum Domain of Attraction (MDA)

The extreme value distributions introduced above represent the limit laws for the normalised maxima of iid random variables. We must consider the conditions on a distribution function F that will give the normalised maxima

5) Write a note on ‘international actuarial notations’.

Ans) Actuarial notation is a shorthand method to allow actuaries to record mathematical formulas that deal with interest rates and life tables.

Traditional notation uses a halo system where symbols are placed as superscript or subscript before or after the main letter. Example notation using the halo system can be seen below.

Various proposals have been made to adopt a linear system where all the notation would be on a single line without the use of superscripts or subscripts. Such a method would be useful for computing where representation of the halo system can be extremely difficult. However, a standard linear system has yet to emerge.

7) What are ‘non-catastrophic losses’? How is the ‘total loss amount’ in respect of such a loss determined?

Ans) In non-catastrophe case, loss amounts depend on the age of insurance contracts. The aging phenomenon describes the fact that the loss ratio - i.e., the ratio of (estimated) total loss divided by earned premiums - decreases when the age of policy increases. For this reason Kaufmann et a1 (2001), divide the insurance business into three classes, viz.,

new business (superscript 0),

renewal business - first renewal (superscript I), and

renewal business - second and subsequent renewals (superscript 2).

There are two main stochastic factors that affect total claim amount. These are: number of losses and severity of losses. The choice of a specific claim number and claim size distribution depends on the line of business and is the result of fitting distributions to empirical data requiring prior adjustments of historical loss data. In the following we will use non-catastrophe losses by referring to a negative binomial (claim number) and a gamma (claim size) distribution.